UVA 1401 Remember the Word

2015-12-05

Problem Description

题目链接：UVA / Remember the Word
难度：提高+ / 省选−

给出一个由 S 个不同单词组成的字典和一个长字符串 Str。把这个字符串分解成若干个单词的连接（单词可以重复使用），有多少种方法？比如，有 4 个单词 a, b, cd, ab，则 abcd 有两种分解方法：a + b + cd 和 ab + cd。

输入包含多组数据，每组数据第一行为待分解的字符串，其长度 L 不超过 300, 000。第二行为单词个数 S，$1\leq S\leq4000$。以下 S 行每行为一个单词，由不超过 100 个小写字母组成。

对每组数据输出方案数模 20, 071, 027。

Thought

Trie 字典树 / 前缀树

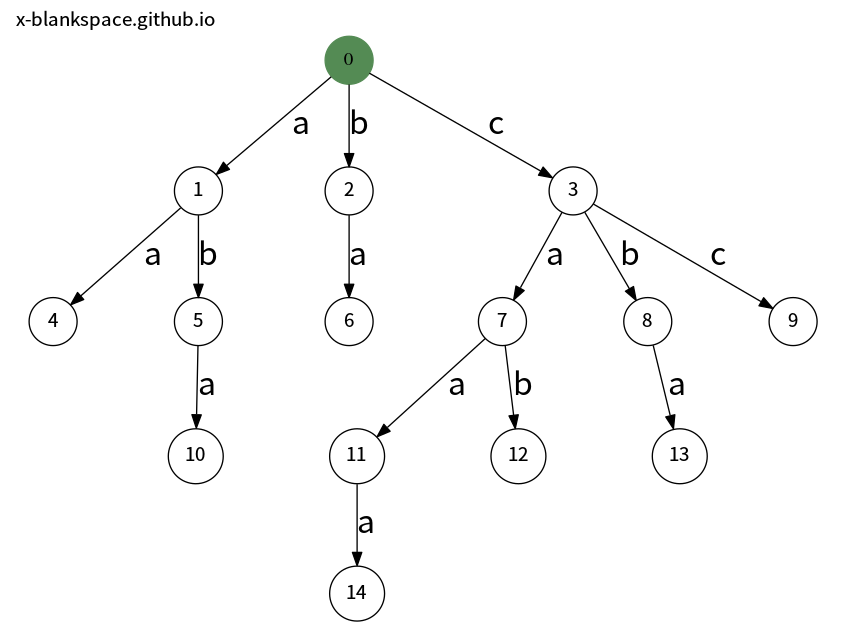
Trie png

$Trie$ 字典树又称前缀树，可以用二维数组 $trie$ 来保存字典树。$trie[node][child]$ 表示节点 $node$ 的第几条潜在的边指向的子节点。具体意思是，由于单词的每个字母的下一个字母都有 26 种可能，对应的是 26 个小写英文字母。但并不是每一种可能都实际存在于字典树中，如果能从 $trie$ 数组中找到下一个节点的序号，就说明存在。

$Trie$ 中从根节点到子节点的路径上的字母就组成了一个个字符串，每个字符串的路径是唯一的。我们可以对其中构成单词的字符串进行标记，具体做法是标记该字符串的最后一个字母指向的节点。例如我们可以设置 isWord[5] = true 这就表示 $ab$ 是单词。

上图表示的字典树是在依次输入以下单词后形成的：$[ a, b, c, aa, ab, ba, ca, cb, cc, aba, caa, cab, cba, caaa ]$

DP 动态规划

令 $dp[i]$ 表示字符串 $Str[i…(len-1)]$ 的分解方案数，也就是从下标 $i$ 开始到字符串结束的分解方案数，显然最终答案就是 $dp[0]$。从后往前递推，边界条件为 $dp[len] = 1$。

$dp[i]$ = $sum${ $dp[i + length(x)]$ | 单词 $x$ 是 $Str[i…(len-1)]$ 的前缀 }

举个例子，如果 $Str = “ababc”$，输入的单词为 $a, ab, b, bc$，那么：

$dp[0] = dp[1] + dp[2]$，对应的两种方案为 $a + babc$，$ab + abc$
$dp[1] = dp[2]$，对应的方案为 $b + abc$
$dp[2] = dp[3]$，对应的方案为 $a + bc$
$dp[3] = dp[5] = 1$，对应的方案为 $bc + 空字符串（边界）$

💡 发现了吗？这本质上和跳台阶问题是同一类问题，属于跳台阶的变式

最终答案为 $dp[0] = 2$

Code

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

const int MAXNODE = 4000 * 100 + 10, MAXCHILD = 26;
const int MAXSTRLEN = 300000 + 10, MAXWORDLEN = 100 + 5;
const int MOD = 20071027;

int trie[MAXNODE][MAXCHILD], globalNode;
bool isWord[MAXNODE];
int dp[MAXSTRLEN];
char word[MAXWORDLEN], str[MAXSTRLEN];

int idx(char c){
    return c - 'a';
}

void init(){
    globalNode = 0;	// 从根节点开始
    memset(trie, 0, sizeof(trie));
    memset(isWord, 0, sizeof(isWord));
    memset(dp, 0, sizeof(dp));
}

void insert(char *word){
    int node = 0, n = strlen(word);
    for(int i = 0; i < n; i++){
        int child = idx(word[i]);
        if(!trie[node][child]){
            trie[node][child] = ++globalNode;
        }
        node = trie[node][child];
    }
    isWord[node] = true;
}

void calcNumOfPlans(char *str){        // 递推
    int len = strlen(str);
    dp[len] = 1;	// 边界
    for(int i = len - 1; i >= 0; i--){
        int node = 0, j = i;
        while(j <= len - 1){
            int child = idx(str[j]);
            node = trie[node][child];
            if (!node) break;
            if(isWord[node]) dp[i] += dp[j + 1], dp[i] %= MOD;
            j++;
        }
    }
}

int main(){
    int n, kase = 0;
    while(~scanf("%s", str)){
        init();

        scanf("%d", &n);
        for(int i = 0; i < n; i++) {
            scanf("%s", word);
            insert(word);
        }

        calcNumOfPlans(str);

        printf("Case %d: %d\n", ++kase, dp[0] % MOD);
    }
    return 0;
}